Rotary Position Embeddings (RoPE)- Intuition, Math, and Examples

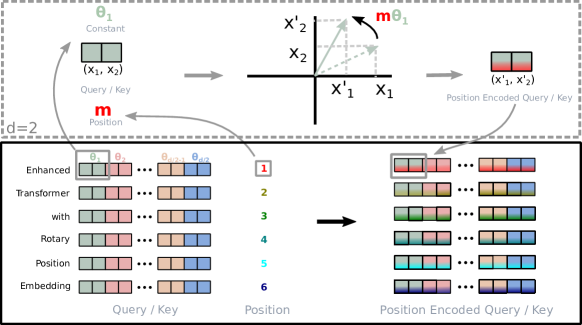
Rotary Position Embeddings (RoPE) diagram

What is RoPE, in one line?

Instead of adding positional vectors to token embeddings, RoPE weaves position directly into the vectors by rotating them in paired 2D subspaces. This makes attention scores depend on relative positions without changing the attention formula.

The journey to RoPE: how we got here

No positional information (the problem): Self-attention is permutation-invariant; without positions, “The cat chased the dog” ≈ “The dog chased the cat”.
Absolute positional embeddings (first solution): Add a fixed/learned vector for each absolute index to token embeddings. Works, but generalizes poorly beyond training length and does not express relative offsets naturally.
Relative positional embeddings (improvement): Add biases to attention scores based on token distance. Captures relative order but complicates attention mechanics.
RoPE (elegant fusion): Rotate queries/keys before the dot product. After rotation, their dot product depends on relative distance, so standard attention natively uses relative positions.

A small, concrete math walkthrough

Model dimension: (d = 4)
Position: word is at (m = 2)
Query vector: (q = [1.0,\ 2.0,\ 3.0,\ 4.0])
Base: (\Theta = 10000)

RoPE treats the embedding as 2D pairs:

Pair (k=1): ((q_0, q_1) = (1.0, 2.0))
Pair (k=2): ((q_2, q_3) = (3.0, 4.0))

Angles per pair use multi-frequency scaling. A common parameterization is: [\theta_{m,k} = m \cdot \Theta^{-(2k-2)/d}.]

For (k=1): (\theta_{2,1} = 2 \cdot 10000^{-(0)/4} = 2) radians
For (k=2): (\theta_{2,2} = 2 \cdot 10000^{-2/4} = 2/\sqrt{10000} = 0.02) radians

Apply a 2D rotation to each pair with the standard rotation matrix. For a pair ((x, y)) and angle (\theta): [\begin{pmatrix}x’\y’\end{pmatrix} = \begin{pmatrix}\cos\theta & -\sin\theta\ \sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}x\y\end{pmatrix}.]

Pair 1 rotated by (2) rad:
- (\cos 2 \approx -0.416), (\sin 2 \approx 0.909)
- (q’_0 = 1.0\cdot(-0.416) - 2.0\cdot 0.909 = -2.234)
- (q’_1 = 1.0\cdot 0.909 + 2.0\cdot(-0.416) = 0.077)
Pair 2 rotated by (0.02) rad:
- (\cos 0.02 \approx 0.9998), (\sin 0.02 \approx 0.02)
- (q’_2 = 3.0\cdot 0.9998 - 4.0\cdot 0.02 = 2.9194)
- (q’_3 = 3.0\cdot 0.02 + 4.0\cdot 0.9998 = 4.0592)

Final rotated vector: (q’ = [-2.234,\ 0.077,\ 2.9194,\ 4.0592]).

This vector now encodes both meaning and position (m=2) in a way attention can use.

Why attention with RoPE depends on relative positions

Consider a single 2D pair from a query at position (m) and a key at position (n). After rotation by angles (\theta_m) and (\theta_n), their dot product simplifies via trig identities to include (\cos(\theta_m - \theta_n)). Because (\theta_m - \theta_n) is proportional to (m - n), the dot product depends on relative distance. Standard attention then automatically leverages relative positions without any custom bias terms.

Why not rotate the whole vector by the same angle?

If you apply the same rigid rotation to all dimensions of both query and key, the dot product is invariant: [(R_\theta q)^\top (R_\theta k) = q^\top (R_\theta^\top R_\theta) k = q^\top k.] No positional signal survives. RoPE instead rotates independent 2D pairs with a spectrum of angles (frequencies). Early pairs use higher frequencies (sensitive to small position changes), later pairs use lower frequencies (capture long-range structure). This multi-frequency design preserves semantics while injecting rich positional cues.

What are (m) and (k)? Will this “break” the word embedding?

(m): the token position index in the sequence (0-based or 1-based as defined by the implementation).
(k): the pair index over the embedding; with (d) even, there are (d/2) pairs: ((0,1)\to k=1), ((2,3)\to k=2), …, ((d-2,d-1)\to k=d/2).

RoPE does not randomly distort the embedding. It applies a consistent, deterministic rotation pattern that the model can learn to factor out from pure semantics. Intuitively, the model sees a token’s meaning plus a stable positional “overlay”; across data, it learns which parts encode meaning and which parts encode position.

Analogy: Think of the embedding as a key with many notches. RoPE tweaks each notch by a predictable amount based on position. All tokens at the same position get the same notch tweaks. The model learns the rulebook for those tweaks and thus keeps meaning intact while also perceiving position.

Is the pairing fixed to 2 dimensions?

Yes. RoPE is built on 2D rotations. Each pair ((x, y)) forms a plane for a standard rotation matrix; equivalently, treat ((x, y)) as a complex number and multiply by (e^{i\theta}). While other schemes are conceivable, the practical, widely used RoPE formulation uses fixed 2D pairs throughout the embedding.

Quick reference: tiny Python helper to rotate pairs

import math

def rotate_pair(x, y, theta):
    c, s = math.cos(theta), math.sin(theta)
    return x * c - y * s, x * s + y * c

def rope_rotate(vec, m, base=10000.0):
    # vec length must be even
    d = len(vec)
    out = [0.0] * d
    for k in range(d // 2):
        i, j = 2 * k, 2 * k + 1
        theta = m * (base ** (-(2 * k) / d))
        out[i], out[j] = rotate_pair(vec[i], vec[j], theta)
    return out

print(rope_rotate([1.0, 2.0, 3.0, 4.0], m=2))

Takeaways

RoPE encodes position via rotations of 2D pairs; attention then reads relative distance naturally.
Multi-frequency angles across pairs let the model represent both short- and long-range positional structure.
Semantics are preserved because the rotational pattern is consistent and learnable, not random.